| Das Folgende geht auf
Untersuchungen zurück, die Nicolas Kauffmann und Jörg Siewerth 1981 als jugendliche Gymnasiasten in Hohenbrunn bei München durchgeführt haben. Die entsprechenden Aufzeichnungen stammen vom 26. und 27.10.1981 |
| Anregungen, Kommentare, BEWEISE, Diskussionsbedarf? → FORUM! |
Division durch Null
Division durch Null?
Geht nicht!
Warum nicht?
Ist nicht definiert!
Warum?
Null
Null: Etwa ein Unendlichstel: 0 ≈ 1/∞
(von der positiven Seite)
(von der positiven Seite)
Null: Etwa ein Minus-Unendlichstel: 0 ≈ 1/-∞
(von der negativen Seite)
(von der negativen Seite)
Null: Sowohl ein Unendlichstel als auch ein Minus-Unendlichstel:
1/-∞ ≈ 0 ≈ 1/+∞
1/-∞ ≈ 0 ≈ 1/+∞
Eins durch Null
Eins durch Null:
Eins durch ein Unendlichstel:
1/0 ≈ 1/1/∞ (von der positiven Seite)
1/0 ≈ 1/1/∞ (von der positiven Seite)
Eins durch Null:
Eins durch ein Minus-Unendlichstel:
1/0 ≈ 1/1/-∞ (von der negativen Seite)
1/0 ≈ 1/1/-∞ (von der negativen Seite)
Doppelbruch:
1/1/∞ = ∞ , 1/1/-∞ = -∞
⇒ -∞ ≈ 1/0 ≈ ∞
Aber das kann ja nun nicht sein, dass -∞ = +∞ ?!
Deswegen ist es nicht definiert.
Zahlenkreis
Oder -∞ ist tatsächlich dasselbe wie +∞ ,
oder besser gesagt: 1/0 = -∞ = +∞ ist genauso neutral
(weder positiv noch negativ) wie 0 !
oder besser gesagt: 1/0 = -∞ = +∞ ist genauso neutral
(weder positiv noch negativ) wie 0 !
Unsinn.
∞ und -∞ treffen sich in 1/0 — die Zahlen
bilden einen Zahlenkreis!
bilden einen Zahlenkreis!
Alter Hut: Riemannsche Zahlenkugel. Komplexe Zahlen.
Abbildung auf die Kugel durch Sekanten von der Ebenenkoordinate
zum ∞-Pol der Kugel.
Abbildung auf die Kugel durch Sekanten von der Ebenenkoordinate
zum ∞-Pol der Kugel.
Warum nicht wie ein Einheitskreis?
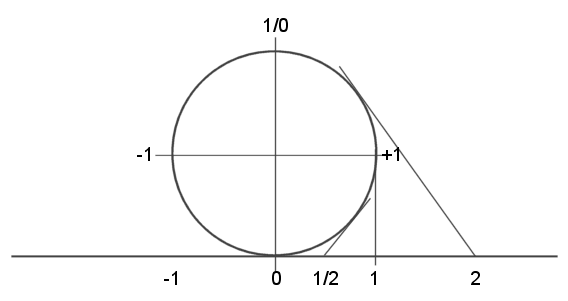
Einheitskreis
Kreis der reellen Zahlen. Ausgehend vom Zahlenstrahl.
(Keine komplexe Zahlenebene.)
(Keine komplexe Zahlenebene.)
Der untere Pol ist 0, der obere Pol 1/0.
Der rechte Pol ist 1, der linke Pol ist -1.
Der rechte Pol ist 1, der linke Pol ist -1.
Der Kreis hat den Radius r = 1.
Die 1 auf dem Kreis liegt senkrecht über der 1 des Zahlenstrahls.
Der Winkel von 0 bis 1 beträgt im Kreis 90° bzw. π/2 .
Die 1 auf dem Kreis liegt senkrecht über der 1 des Zahlenstrahls.
Der Winkel von 0 bis 1 beträgt im Kreis 90° bzw. π/2 .
Abbildungsvorschrift
Geometrisch:
Tangente vom Punkt des Zahlenstrahls an den Kreis.
Tangente vom Punkt des Zahlenstrahls an den Kreis.
Trigonometrisch:
Zahlenstrahl → Kreis: α(x) = 2 arctan x
Kreis → Zahlenstrahl: x(α) = tan(α/2)
Zahlenstrahl → Kreis: α(x) = 2 arctan x
Kreis → Zahlenstrahl: x(α) = tan(α/2)
Der Kreiswinkel wird von der 0 ab gemessen: α(0) = 0 (0π, 0°)
Zum Beispiel:
x(2π/3) = √3 ⇔ α(√3) = 2π/3 (=120°)
x(π/3) = 1/√3 ⇔ α(1/√3) = π/3 (=60°)
x(3π/4) = √2 + 1 ⇔ α(√2) = 3π/4 (=135°)
x(π/4) = √2 - 1 (= 1/(√2 + 1)) ⇔ α(√2 - 1) = π/4 (=45°)
x(2π/3) = √3 ⇔ α(√3) = 2π/3 (=120°)
x(π/3) = 1/√3 ⇔ α(1/√3) = π/3 (=60°)
x(3π/4) = √2 + 1 ⇔ α(√2) = 3π/4 (=135°)
x(π/4) = √2 - 1 (= 1/(√2 + 1)) ⇔ α(√2 - 1) = π/4 (=45°)
Eigenschaften
Die beiden vorzeichenlosen bzw. vorzeichenneutralen Pole
des Kreises (0 und 1/0) liegen auf der senkrechten Mittelachse,
genau übereinander.
des Kreises (0 und 1/0) liegen auf der senkrechten Mittelachse,
genau übereinander.
Der Kehrwert einer beliebigen Zahl selben Vorzeichens liegt
genau senkrecht auf der gegenüber liegenden oberen oder unteren
Hälfte des Kreises.
Z.B.: α(√3) = 120° und α(1/√3) = 60° (sin 120° = sin 60°).
genau senkrecht auf der gegenüber liegenden oberen oder unteren
Hälfte des Kreises.
Z.B.: α(√3) = 120° und α(1/√3) = 60° (sin 120° = sin 60°).
1 und -1 liegen auf der waagrechten Mittelachse,
genau einander gegenüber. (Sie sind ja auch die einzigen
2 Zahlen, deren Kehrwert wieder sie selbst ergibt...)
genau einander gegenüber. (Sie sind ja auch die einzigen
2 Zahlen, deren Kehrwert wieder sie selbst ergibt...)
Die Negation einer beliebigen Zahl liegt genau waagrecht
auf der gegenüber liegenden Hälfte des Kreises.
auf der gegenüber liegenden Hälfte des Kreises.
Die Tangente selbst hat vom Punkt x auf dem Zahlenstrahl
bis zum Winkel α auf dem Kreis die Länge x des entsprechenden
Zahlenstrahl-Abschnitts.
(Steche einen Zirkel bei x auf dem Zahlenstrahl ein und ziehe
den Bogen vom 0-Punkt zu α auf dem Kreis.)
bis zum Winkel α auf dem Kreis die Länge x des entsprechenden
Zahlenstrahl-Abschnitts.
(Steche einen Zirkel bei x auf dem Zahlenstrahl ein und ziehe
den Bogen vom 0-Punkt zu α auf dem Kreis.)
Trigonometrische Wurzelfunktion
Kann man die Wurzel √ auch anders darstellen?
Ja, durch gebrochene Exponenten.
Und z.B. trigonometrisch?
Ist nicht bekannt.
Die Wurzelfunktion
√x = tan( (arcsin( tan(arctan(x) - π/4)) + π/2) /2 )
Kann man das kürzen / vereinfachen?
Ich kenne mich mit Trigonometrie leider nicht so gut aus.
(Info bitte an n punkt kauffmann ät gmx punkt de)
Ich kenne mich mit Trigonometrie leider nicht so gut aus.
(Info bitte an n punkt kauffmann ät gmx punkt de)
Geometrische Entwicklung
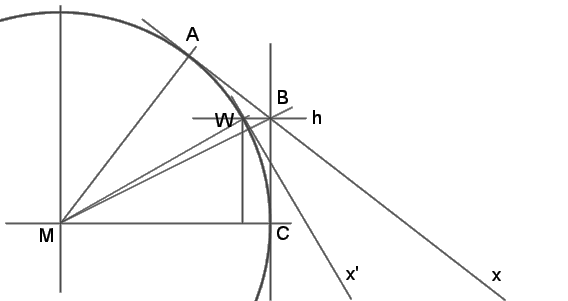
Vom Schnittpunkt (B) der x-Tangente mit der 1-Tangente wird
eine Hilfslinie (h) waagrecht auf den Kreis gezogen.
Der Schnittpunkt (W) der Hilfslinie mit dem Kreis markiert den
entsprechenden Winkel von √x (Berührungspunkt der Tangente x').
eine Hilfslinie (h) waagrecht auf den Kreis gezogen.
Der Schnittpunkt (W) der Hilfslinie mit dem Kreis markiert den
entsprechenden Winkel von √x (Berührungspunkt der Tangente x').
Herleitung
Hier wird nur die Entwicklung der Formel hergeleitet.
Dass oder warum die Formel stimmt, steht hier nicht.
Dass oder warum die Formel stimmt, steht hier nicht.
Behauptet:
α(√x) = ∠WMC + π/2
(⇒ √x = tan( ∠WMC/2 + π/4) )
α(√x) = ∠WMC + π/2
(⇒ √x = tan( ∠WMC/2 + π/4) )
Gesucht:
Winkel ∠WMC (um über die Tangente x' an W die Wurzel von x
auf dem Zahlenstrahl zu erhalten)
Strecke BC = tan (∠BMC)
⇒ ∠WMC = arcsin BC = arcsin( tan (∠BMC) )
Winkel ∠WMC (um über die Tangente x' an W die Wurzel von x
auf dem Zahlenstrahl zu erhalten)
Strecke BC = tan (∠BMC)
⇒ ∠WMC = arcsin BC = arcsin( tan (∠BMC) )
Gegeben:
∠AMC = α - π/2 (π/2 ist das untere rechte Kreisviertel)
∠BMC = (∠AMC)/2 (Δ MAB in A rechtwinklig, kongruent zu
Δ MCB in C rechtwinklig, daher teilt MB ∠AMC genau mittig)
⇒ ∠BMC = (α - π/2)/2 = α/2 - π/4
∠AMC = α - π/2 (π/2 ist das untere rechte Kreisviertel)
∠BMC = (∠AMC)/2 (Δ MAB in A rechtwinklig, kongruent zu
Δ MCB in C rechtwinklig, daher teilt MB ∠AMC genau mittig)
⇒ ∠BMC = (α - π/2)/2 = α/2 - π/4
Gefolgert:
α(√x) = arcsin( tan( α/2 - π/4) ) + π/2
Und da α = 2 arctan x :
α(√x) = arcsin( tan( arctan(x) - π/4) ) + π/2
√x = tan( (arcsin( tan(arctan(x) - π/4)) + π/2) /2 )
α(√x) = arcsin( tan( α/2 - π/4) ) + π/2
Und da α = 2 arctan x :
α(√x) = arcsin( tan( arctan(x) - π/4) ) + π/2
√x = tan( (arcsin( tan(arctan(x) - π/4)) + π/2) /2 )
Abweichung oder Rundungsfehler?
Wir haben damals mit dem Taschenrechner gerechnet und
verglichen und heute nehme ich dafür Excel, um zwischen
der eingebauten Wurzel und unserer Formel zu vergleichen.
verglichen und heute nehme ich dafür Excel, um zwischen
der eingebauten Wurzel und unserer Formel zu vergleichen.
Im Bereich von 0,01 ≤ x ≤ 80 gibt Excel beim Vergleich
zwischen konventionellem und trigonometrischen "Wurzelziehen"
keine Abweichungen an.
zwischen konventionellem und trigonometrischen "Wurzelziehen"
keine Abweichungen an.
Hier eine kleine Übersicht:
| x | √x | Abweichung |
|---|---|---|
| 0,0000000001 (= 1E-10) | 0,00001 | 4,14179E-13 (= 0,000000000000414179) |
| 0,000016 | 0,004 | 3,60562E-15 (= 0,00000000000000360562) |
| 0,01 | 0,1 | 0 |
| 64 | 8 | 0 |
| 10.000 | 100 | 3,67493E-11 (= 0,0000000000367493) |
| 25.000.000 | 5.000 | 1,54196E-06 (= 0,00000154196) |
Beweis?
Ist's nun wirklich die Wurzelformel oder nur eine Annäherung?
Wer will's beweisen? Freiwillige vor!
(Ich kann's nicht.)
Wer will's beweisen? Freiwillige vor!
(Ich kann's nicht.)
© Nicolas Kauffmann & Jörg Siewerth
| Anregungen, Kommentare, BEWEISE, Diskussionsbedarf? → FORUM! |